Demonstração da Fórmula do Volume do Tronco de Pirâmide
Analisando a pirâmide abaixo, podemos relacionar algumas semelhanças:

Analisamos separadamente o triângulo retângulo: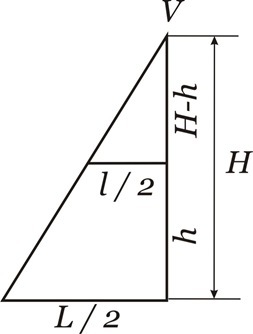
Por semelhança de triângulos, temos:
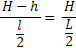


Se elevarmos ao quadrado, termos:

Como L2 e l2 são as áreas das bases das pirâmides maior e menor, respectivamente, reescrevemos como:

Denomina-se tronco de pirâmide de bases paralelas a parte da pirâmide limitada por sua base e por uma secção transversal qualquer desta pirâmide.
O volume V do tronco de pirâmide é obtido pela diferença dos volumes das pirâmides:

Já foi demonstrado como obter o Volume V de uma pirâmide, então temos que:

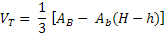


Utilizando da propriedade da secção transversal, podemos determinar o valor da altura H em função de AB, Ab e h :
![clip_image007[1] clip_image007[1]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEhmH0IUWYUp7TZwbAKhh3KNkJAOqmDs3zO4YWIusqw85uw7T1BUdqB28HIcSW4uyVSTnu9xSuVH4pldbOr0WqvOsVmd71Z5nQs-rGJGlTZdDcLj0JKijyPY-Zx5BV-Y7jXCplGXBbBQAhaf/?imgmax=800)
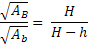



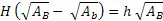
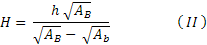
Substituindo ( II ) em ( I ), temos:

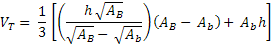





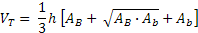
Pronto. Esta é a fórmula para o cálculo do Volume de um Tronco de Pirâmide

Analisamos separadamente o triângulo retângulo:

Por semelhança de triângulos, temos:

Se elevarmos ao quadrado, termos:
Como L2 e l2 são as áreas das bases das pirâmides maior e menor, respectivamente, reescrevemos como:
Denomina-se tronco de pirâmide de bases paralelas a parte da pirâmide limitada por sua base e por uma secção transversal qualquer desta pirâmide.
O volume V do tronco de pirâmide é obtido pela diferença dos volumes das pirâmides:
Já foi demonstrado como obter o Volume V de uma pirâmide, então temos que:
Utilizando da propriedade da secção transversal, podemos determinar o valor da altura H em função de AB, Ab e h :
Substituindo ( II ) em ( I ), temos:
Pronto. Esta é a fórmula para o cálculo do Volume de um Tronco de Pirâmide
Nenhum comentário:
Postar um comentário