Uma
empresa precisa comprar uma tampa para seu reservatório, que te a forma
de um tronco de cone circular reto, conforme mostrado na figura.
Considere que a base do reservatório tenha raio r = 2√3 m e que sua lateral faça um ângulo de 60° com o solo.
Se a altura do reservatório é 12 m, a tampa a ser comprada deverá cobrir uma área de
(1) Analisemos a figura da seguinte forma:
É fácil notar que o raio da tampa desse reservatório é dado por: X + 2√3
(2) Analisemos a a parte verde da figura da seguinte forma:
Para encontramos a o "x" da figura acima basta apenas aplicarmos trigonometria no triângulo retângulo.
O raio da tampa desse reservatório é dado por:
X + 2√3 = 4√3 + 2√3 = 6√3
A área da tampa do reservatório é dada por:
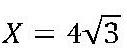
Nenhum comentário:
Postar um comentário