Se um cone sofrer a intersecção de um
plano paralelo à sua base circular, a uma determinada altura, teremos a
constituição de uma nova figura geométrica espacial denominada Tronco de
Cone.
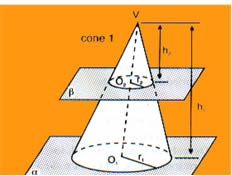
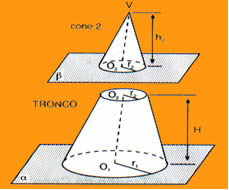
Observe que, diferentemente do cone, o
tronco de cone possui duas bases circulares em que uma delas é maior que
a outra, dessa forma, os cálculos envolvendo a área superficial e o
volume do tronco envolverão a medida dos dois raios. A geratriz, que é a
medida da altura lateral do cone, também está presente na composição do
tronco de cone.
Não devemos confundir a medida da altura
do tronco de cone com a medida da altura de sua lateral (geratriz), pois
são elementos distintos. A altura do cone forma com as bases um ângulo
de 90º. No caso da geratriz os ângulos formados são um agudo e um
obtuso.
h = altura
g = geratriz
g = geratriz
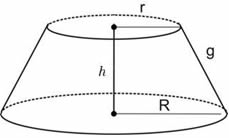
As fórmulas referentes ao cálculo da área superficial e do volume são as seguintes:
Área Superficial
Volume


Exemplo 1
Os raios das bases de um tronco de cone
são 6 m e 4 m. A altura referente a esse tronco é de 10 m. Determine o
volume desse tronco de cone. Lembre-se que π = 3,14.
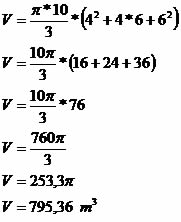
Exemplo 2
Um tronco de cone possui a medida dos
raios igual a 5 m e 8 m. Sabendo que a medida da altura é igual a 4,
determine a área superficial desse sólido.
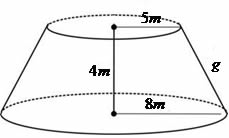
Para determinarmos a área superficial devemos calcular a geratriz desse tronco de cone. Observe o cálculo realizado:
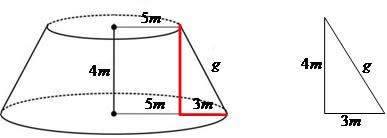
Utilizando o Teorema de Pitágoras temos:
g² = 4² + 3²
g² = 16 + 9
g² = 25
√g² = √25
g = 5
g² = 16 + 9
g² = 25
√g² = √25
g = 5
Calculando a área superficial
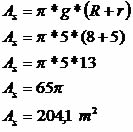
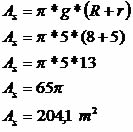
Nenhum comentário:
Postar um comentário