Gerônimo
Cardano, médico e matemático
italiano, publicou em 1545, em sua obra Ars magna, a resolução de
equações do tipo x³ + px +
q = 0. Essa resolução, relata
Cardano, foi apresentada a ele por Nicolo Tartáglia. O método proposto
por Tartáglia consiste
em substituir a variável x por u – v
tal que o produto uv seja um terço do coeficiente de x da equação.
Cardano, resolvendo
equações cúbicas através desse
método, deparou-se com raízes quadradas de números negativos, que até
então não eram aceitas
pelos matemáticos. Vamos percorrer o
mesmo caminho feito por Cardano para perceber algo surpreendente.
Resolvamos a seguinte
equação:
x³
- 6x + 4 = 0
Substituindo
x por u – v de modo que o produto uv
seja igual a um terço do coeficiente de x, que é -2 , obtém-se o
sistema
(u
– v)³ - 6(u – v) + 4 = 0
uv
= -2
u³
- 3u²v + 3uv² - v³ - 6u + 6v + 4 = 0
uv
= -2
Fazendo
uv = -2 na primeira equação e isolando v na segunda , obtém-se:
u³
- v³ + 4 = 0
v
= -2/u
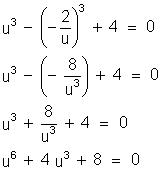
Chamando
u³ = t temos:
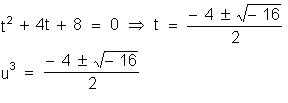
Nesse
momento, Cardano concluiu: como não
existe raiz quadrada de número negativo, temos que não existem u nem v
e, conseqüentemente,
não existe x, pois x = u – v. Porém,
espantosamente ele verificou que o número real 2 é raiz da equação
x³
- 6x + 4 = 0, pois 2³ - 6.2 + 4 = 0.
Essa
constatação levou Cardano a considerar a existência de novos números, como por exemplo:
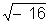
Nessa
mesma época, outro grande matemático italiano, Rafael Bombelli ( cerca de
1526
– 1573), teve o que chamou de “idéia
louca”, operando com expressões que envolviam raízes quadradas de
números
negativos. Bombelli admitiu, por
exemplo, a identidade:
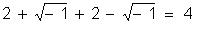
Dando
assim subsídios para o início da construção de um novo conjunto: o conjunto dos números
complexos.
Até
agora, o conjunto universo utilizado
na resolução de problemas e equações foi o conjunto R dos números
reais. Algumas equações
não tinham solução no conjunto dos
reais. É o caso, por exemplo, da equação x² + 1 = 0
x²
+ 1 = 0
x²
= -1
S
= { }
Agora, veja que, se tomarmos como universo um conjunto para o qual se admita a existência de raiz
quadrada de -1 a equação passará a ter solução não-vazia.
No conjunto dos números complexos,convenciona-se
que:

Exemplo:
Vamos
resolver a equação x² - 2x + 5 = 0.
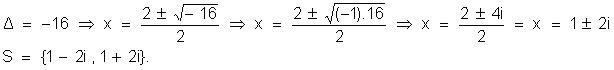
Conjunto dos números complexos é aquele formado
pelos números que podem ser expressos na forma z = a + bi , em que:
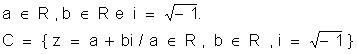
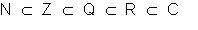
A forma z = a + bi é denominada forma algébrica de um número complexo,
em que a é a parte real e b, a parte
imaginária.
Tomando
um número complexo z = a + bi, temos:
a
= 0 z = a + bi
b ≠ 0 (imaginário puro).
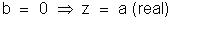
Dessa
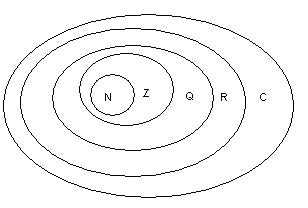
maneira, todo número real pode ser expresso na forma
a
+ bi com b = 0. Isso nos permite concluir que todo número real é também complexo.
Exemplo:
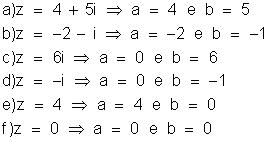
Os
complexos 6i e –i são imaginários puros e os complexos 4 e 0 são reais.
Exercícios:
Classifique
cada número complexo a seguir como imaginário puro ou real:
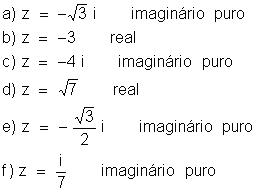
Determine
o valor de m e n para que o complexo
z
= (m² - 4) + (n³ - 27) i seja um imaginário puro.
Resolução:
z
= a + bi é imaginário puro se a = 0 e b ≠ 0. Logo:
m²
- 4 = 0
m²
= 4
m
= -2 ou m = 2
n³
- 27 ≠ 0
n³
≠ 27
n
≠ 3
Dados
os complexos a seguir, determine:
a)
m e n para que z = m + (2m - n + 1)i seja imaginário puro.
Resolução:
m
= 0
2m
– n + 1 ≠ 0
-n
≠ -1
n
≠ 1
b)
a e b para que z = (4a – 5) + (2b + 7)i seja real.
Resolução:
2b
+ 7 = 0
qualquer a є R
2b
= -7
b
= - 7/2
c)
x e y para que z = (2x + 4) – (y – 3) i seja o real z = 0.
Resolução:
2x
+ 4 = 0
y – 3 = 0
2x
= -4
y = 3
x
= -4/2 = -2
Resolva
as equações a seguir para U = C:
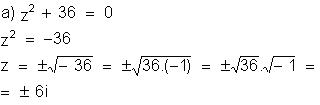
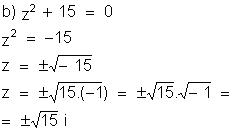
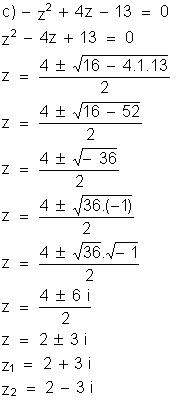
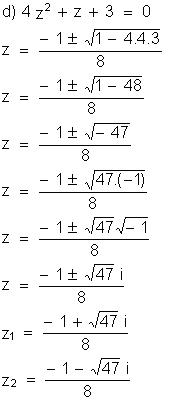
Igualdade
e operações
Dados
dois números complexos z1 = a1 + b1i e z2 = a2 + b2i, dizemos
que eles são iguais quando a parte real de z1 for igual a de z2, o mesmo ocorrendo com as partes imaginárias:
a1
+ b1i = a2 + b2i ↔ a1 =
a2 e b1 = b2
Exemplo:
Considere
os complexos z1 = (a + 1) + 3i e z2 = 4 + (2 – b) i. Teremos z1 = z2 se
ocorrer:
(a
+ 1) + 3i = 4 + (2 – b) i
a
+ 1 = 4
a
= 3
2
– b = 3
b
= -1
Adição
e subtração
Faz-se
a adição ou a subtração dos complexos z1 = a1 + b1i e
z2
= a2 + b2i somando ou subtraindo as partes reais, a1 e a2 e as partes imaginárias b1 e b2:
(a1
+ b1i) + (a2+ b2i) = (a1+ a2) + (b1+ b2)
i
(a1
+ b1i) - (a2 + b2i) = (a1 - a2 ) + (b1 - b2)
i
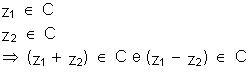
Dados os complexos z1 = 2 –
3i e z2 = z2 = 4 + 6i, temos:
a) z1 + z2 = 2 – 3i + 4 + 6i = 6 + 3i
b) z1 - z2 = 2 – 3i –
( 4 + 6i ) = -2 – 9i
c)z2 – z1 =
4 + 6i – ( 2 – 3i ) = 2 + 9i
d)2z1= z1 + z1 = 2 – 3i + 2 – 3i = 4 – 6i
e)2z2 = z2 + z2
= 4 + 6i + 4 + 6i = 8 + 12i
Efetue as operações indicadas:
a)(6 + 5i)
+ (3 – 4i) = 6 + 5i + 3 – 4i = (6 + 3) + (5 – 4)i = 9 + i
b)(1 –
i) – (3 – 2i) = 1 – i – 3 + 2i = (1 – 3) + (2 – 1)i = -2 + i
Multiplicação
Na multiplicação dos complexos z1 = a1 + b1i e z2 = a2 + b2i,
procede-se como na multiplicação de dois binômios, fazendo
i² = -1. Assim:
z1 = a1 + b1i
z2 = a2 + b2i
z1 . z2 = (a1 +
b1i).( a2 + b2i)
z1 . z2 = a1a2
+ a1b2i + a2 b1i + b1 b2i²
Como i² = -1, temos:
(a1 + b1i).( a2 +
b2i) = (a1a2 - b1 b2) + (a1b2 + a2
b1) i
Exemplos:
Vamos multiplicar z1 = 3 + 2i por
z2 = 3 + 4i
z1 . z2 = (3 + 2i )( 3
+ 4i) = 9 + 12i + 6i + 8i² = 9 + 18i + 8(-1) =
9 + 18i – 8 = 1 + 18i
Se z1 = 4 e z2 = 2 - 5i, temos:
z1 . z2 = 4(2 – 5i)
= 8 – 20i
Pode ocorrer também que o produto de dois números
complexos seja um número real:
z1 = 2 + i
z2 = 2 – i
z1 . z2 = (2 + i) (2 –
i) = 4 – i² = 5
Dados z1 = 1 – 3i e z2
= 2 + i, calcule:
a) z1 . z2
z1 . z2 = (1 – 3i)(2 + i) = 2 + i
– 6i – 3i² = 2 – 5i + 3 = 5 – 5i
b) 2z1 - 3z2
2z1
- 3z2 = 2(1 – 3i) – 3(2 + i) = 2 – 6i – 6
– 3i = - 4 – 9i
c) z1²
(1 – 3i)² = 1 – 6i + 9i² = 1 – 6i – 9 = - 8
– 6i
d) z2²
(2 + i)² = 4 + 4i + i² = 4 + 4i – 1 = 3 + 4i
e) (z1 + z2)( z1
- z2)
(1 – 3i + 2 + i)[1 – 3i – (2 + i)] =
= (3 – 2i)[1 – 3i – 2 – i] = (3 – 2i)[-1 – 4i] =
= -3 – 12i + 2i + 8 i² = -3 – 12i + 2i – 8 = -11 – 10i
Dados os complexos z1 = a + 2i e z2 = 3 – bi, determine a e b para que 2z1 - z2
seja um imaginário puro.
Resolução:
z1 = a + 2i
z2 = 3 – bi
2z1 - z2 = 2(a + 2i) –
(3 – bi) = 2a + 4i – 3 + bi =
= (2a – 3) + (4 + b)i
Para 2z1
- z2 seja um imaginário puro devemos impor:
2a – 3 = 0
2a = 3
a = 3/2
4 + b ≠ 0
b ≠ - 4
Calcule o valor do número z = (5 – i)²
+ (5 + i)².
Resolução:
z = 25 – 10i + i² + 25 + 10i + i² = 25
– 10i – 1 + 25 + 10i – 1 = 48
Determine o valor real de x para que o número
complexo:
z = (1 – 2x) + 3i seja um número imaginário
puro.
Para que z seja um imaginário puro é necessário
que Re(z) = 0,
Pois Im(z) = 3 ≠ 0
Então:
1 – 2x = 0
-2x = -1
x = 1/2
verificando, vem:
z = (1 – 2x) + 3i = (1-2.1/2) + 3i = 0
+ 3i = 3i (imaginário puro)
logo, x = 1/2
z = (8 – x) + (2x – 3)i seja um número
imaginário puro.
8 – x = 0
x = 8
para x = 8, temos:
(2.8 – 3) = 13 ≠ 0
Logo, x = 8
Conjugado de um complexo
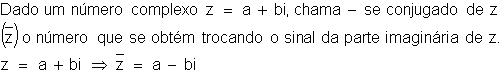
Vamos
obter os conjugados dos seguintes números:
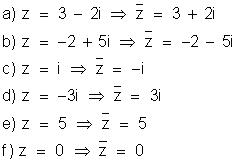
Divisão
Dados os complexos z1 e z2 com z2 ≠ 0, podemos fazer
z1
/z2 multiplicando o numerador e o denominador da fração
pelo conjugado do denominador.
Considere z1 = a1 + b1i
e z2 = a2 + b2i.
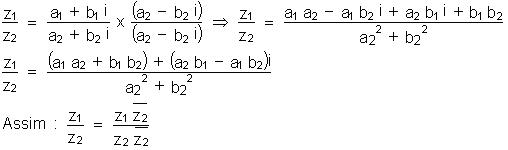
Exemplos:
Vamos efetuar a divisão de z1 = 2
+ 4i por z2
= 5 – i ;
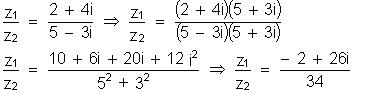
Utilizando
o conjugado de um número z, vamos obter o seu inverso:
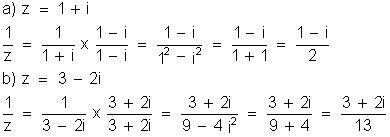
Escreva os conjugados dos seguintes complexos:
z = -3i + 1
conjugado: 1 + 3i

Efetue
as divisões:
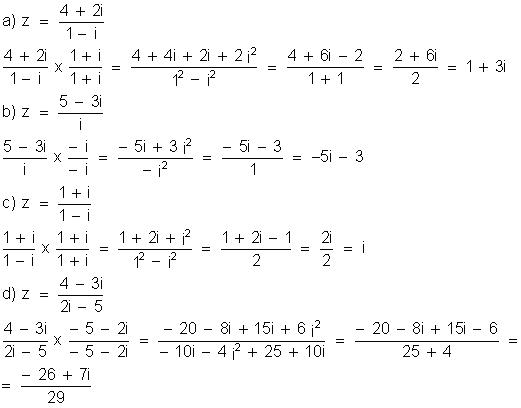

Simplifique
a expressão:
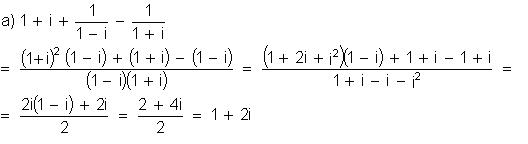
Determine
o número complexo z tal que:
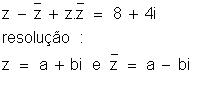
(a
+ bi) – (a – bi) + (a + bi)(a – bi) = 8 + 4i
a + bi – a + bi + a² - abi + abi
– bi² = 8 + 4i
2bi
+ a² + b² = 8 + 4i
2b
= 4
b
= 2
a²
+ b² = 8
a²
+ 4 = 8
a²
= 4
Logo,
z = 2 + 2i ou z = -2 + 2i
Potências
de i
Estudando
as potências de i
Nenhum comentário:
Postar um comentário